
備忘録として臨床研究について学んだことを記します

今回は統計解析で用いられる帰無仮説における平均値の差の分布と
αエラーの関係性について解説致します
.
αエラーとβエラー
臨床研究においては、研究者自身が仮説を検証しようとする際に、2つのものを比べて、その差がどのようになっているかを確認することで、その仮説が確からしいのか否か判断を下すということは、繰り返し述べてきました。
研究者が自身の仮説を検証しようとする際に、2種類の誤った判断を下してしまうことがあります。
.
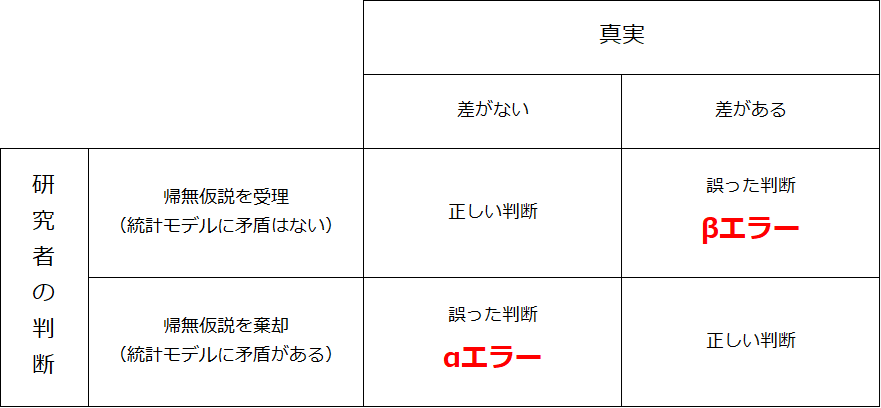
● αエラー:2つのものを比べた際に真実は差がないのに誤って差があると判断してしまう
● βエラー:2つのものを比べた際に真実は差があるのに誤って差がないと判断してしまう
.
.
帰無仮説における平均値の差の分布とαエラーの関係性

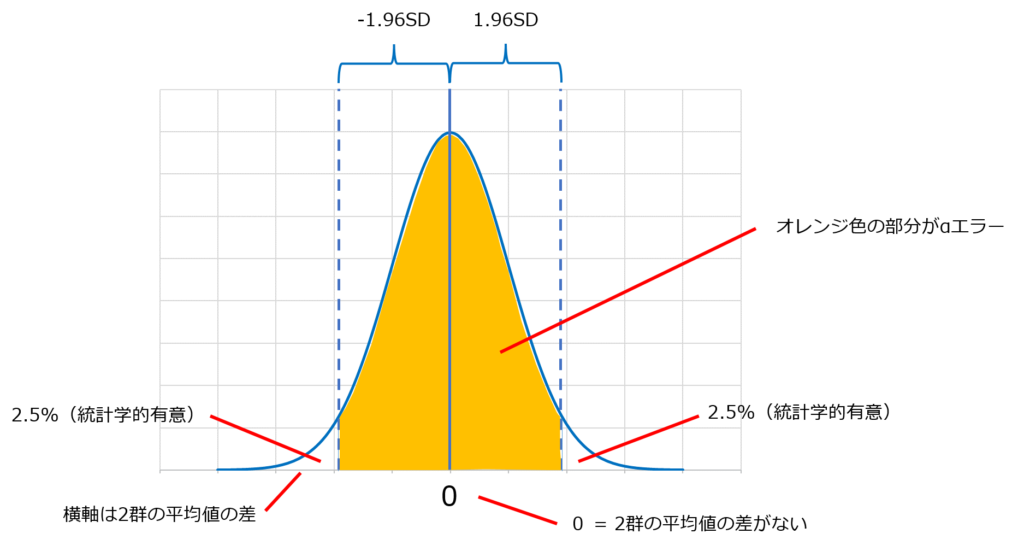
下図は有意水準5%で片側検定を行った場合の、
帰無仮説における平均値の差の分布とαエラーの関係性を示したイメージ図です

ケース群の平均値とコントロール群の平均値の差がオレンジ色の範囲にあるのに
「差がある」と判断する誤りがαエラーです
研究者が臨床研究において、標準的治療方法Bよりも試験的治療方法Aの方が治療効果が高いか否かを確認したとします。
このとき、研究において行われることは、何人かの患者を対象者として試験的治療方法Aの効果の平均値と標準的治療方法Bの効果の平均値の差を求めることです。
効果の平均値の差が0の場合は、AとBの2つの治療方法の効果には文字通り差がないことを意味し、まさしくこれが帰無仮説なのです。
しかし、真の効果の平均値の差が0であったとしても、実際に研究者が得たデータは、研究者が調査したい母集団から無作為に一部の対象者を調査したに過ぎません。
実際の研究で導き出される効果の平均値の差には、真の値(帰無仮説では0)から、いくらかブレてしまう可能性があります。
実際の研究では試験的治療方法Aの効果の平均値と標準的治療方法Bの効果の平均値の差を求めることは1回しか行われませんが、もしも同様の研究を何百回、何千回と繰り返すと、帰無仮説が正しい場合には効果の平均値の差は0を中心として正規分布します。
ただし、研究者が得たデータによるAの効果の平均値とBの効果の平均値の差が図の左端、または右端のそれぞれ2.5%の範囲(=合計5%の範囲)に収まった場合には、「Aの効果の平均値とBの効果の平均値に差がないという仮説に矛盾があると判断します」と予め決めておくわけです。
ちなみに、研究者の本心は、Aの方が効果的であるかを確認したいわけですから、帰無仮説(AとBの効果の平均値の差が0であるという仮説)を否定したいわけです。
このような心理から、Aの効果の平均値とBの効果の平均値が差が図のオレンジ色の範囲に収まり、本来「差がない」と判断しなければならないところを、差があると研究者が判断してしまう誤りがαエラーです。
.
最後に

今後も臨床研究に関して学んだことを記していきたいと思います
.
ありがとうございました!!
.
.



コメント